| prev | home | next |
Imagine 400 ft-lbs of torque measured on a chassis dynamometer like a DynoJet (see references at the end). This is a very nice number to have in any car, street or racing. In dyno-speak, however, the interpretation of this number is a little tricky.
To start a dyno session, you strap your car down with the driving wheels over a big, heavy drum, then you run up the gears gently and smoothly until you're in fourth at the lowest usable engine RPM, then you floor it, let the engine run all the way to redline, then shut down. The dyno continuously measures the time and speed of the drum and the engine RPM through a little remote radio receiver that picks up spark-plug noise. The only things resisting the motion of the driving wheels are the inertia of the driveline in the car and the inertia of the drum. The dyno 'knows' the latter, but not the former. Without these inertias loading the engine, it would run up very quickly and probably blow up. Test-stand dynos, which run engines out of the car, load them in different ways to prevent them from free running to annihilation. Some systems use water resistance, others use electromagnetic; in any case, the resistance must be easy to calibrate and measure. We are only concerned with chassis dynos in this article, however.
What is the equation of motion for the car + dyno system? It is a simple variation on the theme of the old, familiar second law of Newton. For linear motion, that law has the form F = ma, where F is the net force on an object, m is its mass, and a is its acceleration, or time rate of change of velocity.
For rotational motion, like that of the driveline and dyno, Newton's second
law takes the form ![]() where T is the net torque on an object, J
is its moment of inertia, and
where T is the net torque on an object, J
is its moment of inertia, and ![]() is its angular
acceleration, or time rate of change of angular velocity.
The purpose of this instalment of the Physics of Racing is to explain
everything here and to run a few numbers.
is its angular
acceleration, or time rate of change of angular velocity.
The purpose of this instalment of the Physics of Racing is to explain
everything here and to run a few numbers.
To get the rotational equation of motion, we assume that the dyno drum is strong enough that it will never fly apart, no matter how fast it spins. We model it, therefore, as a bunch of point masses held to the centre of rotation by infinitely strong, massless cables. With enough point masses, we can approximate the smooth (but grippy) surface of the dyno drum as closely as we would like.
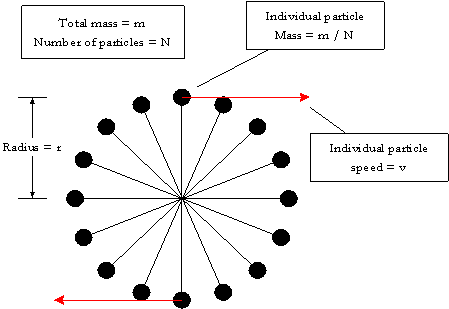
Assume each particle receives a force of F / N in the
tangential direction. Tangential, of course, means the same as circumferential
or longitudinal, as clarified in recent instalments about slip and grip of
tyres. So, each particle accelerates according to F / N = ma / N.
The N cancels out, leaving a = F / m.
Now, a is the rate of change of the velocity, and the velocity is
defined as ![]() , where r is the constant radius of the
circle and
, where r is the constant radius of the
circle and ![]() is the angular velocity in radians per
second. The circumference of the circle is
is the angular velocity in radians per
second. The circumference of the circle is ![]() , by
definition, so a drum of 3-foot radius has a circumference of about 6.28 x 3 =
18.8 feet. At 60 RPM, which is one rev per second, each particle goes 18.8 feet
per second, which is about 15 x 18.8/22 = 12.8 mph. RPM is one measurement of
angular velocity, but it's more convenient to measure it such that
, by
definition, so a drum of 3-foot radius has a circumference of about 6.28 x 3 =
18.8 feet. At 60 RPM, which is one rev per second, each particle goes 18.8 feet
per second, which is about 15 x 18.8/22 = 12.8 mph. RPM is one measurement of
angular velocity, but it's more convenient to measure it such that ![]() angular
units go by every second. Such units save us from having to track factors of
angular
units go by every second. Such units save us from having to track factors of ![]() all
over the math. So, there are
all
over the math. So, there are ![]() radians per revolution, and the
equation
radians per revolution, and the
equation ![]() is seen as a general expression of the example that
is seen as a general expression of the example that ![]() x
revolutions per second = 18.8 feet per second = velocity.
x
revolutions per second = 18.8 feet per second = velocity.
Since r is constant, it has no rate of change. Only ![]() has one, measured in radians per second per second, or radians per second
squared, or
has one, measured in radians per second per second, or radians per second
squared, or ![]() , and denoted with an overdot:
, and denoted with an overdot: ![]() . The equation
of motion, so far, looks like
. The equation
of motion, so far, looks like ![]() . Now, we know that torque is just
force times the lever arm over which the force is applied. So, a force of F
at the surface of the drum translates into a torque of T = Fr applied
to the shaft-or by the shaft, depending on point of view. So we write
. Now, we know that torque is just
force times the lever arm over which the force is applied. So, a force of F
at the surface of the drum translates into a torque of T = Fr applied
to the shaft-or by the shaft, depending on point of view. So we write ![]() ,
which we can rearrange to
,
which we can rearrange to ![]() . We can make this resemble the
linear form of Newton's law if we define
. We can make this resemble the
linear form of Newton's law if we define ![]() , the moment
of inertia of the drum, yielding
, the moment
of inertia of the drum, yielding ![]() , which looks just like F = ma
if we analogise as follows:
, which looks just like F = ma
if we analogise as follows: ![]() .
.
This value for J only works for this particular model of
the drum, with all the mass elements at distance r from the
centre. Suffice it to say that a moment of inertia for any other model of the
drum could be computed in like manner. It turns out that the moment of inertia
of a solid cylindrical drum is half as much, namely ![]() . Moments of
inertia for common shapes can be looked up all over the place, for instance
at http://www.physics.uoguelph.ca/tutorials/torque/Q.torque.inertia.html.
. Moments of
inertia for common shapes can be looked up all over the place, for instance
at http://www.physics.uoguelph.ca/tutorials/torque/Q.torque.inertia.html.
So, now, the dyno has a known, fixed value for J, and it
measures ![]() very accurately. This enables it to calculate trivially just how
much torque is being applied by the driving wheels of the car to the drum. But
it does not know the moment of inertia of the driveline of the car, let
alone the radius of the wheels, the gear selected by the driver, the final-drive
ratio in the differential, and so on. In other words, it knows nothing about the
driveline other than engine RPM.
very accurately. This enables it to calculate trivially just how
much torque is being applied by the driving wheels of the car to the drum. But
it does not know the moment of inertia of the driveline of the car, let
alone the radius of the wheels, the gear selected by the driver, the final-drive
ratio in the differential, and so on. In other words, it knows nothing about the
driveline other than engine RPM.
Everyone knows that the transmission and final-drive on a car multiply the engine torque. The torque at the driving wheels is almost always much larger than the flywheel torque, and it's larger in lower gears than in higher gears. So, if you run up the dyno in third gear, it will accelerate faster than if you run it up in fourth gear. Yet, the dyno reports will be comparable. Somehow, without knowing any details about the car, not even drastic things like gear choice, the dyno can figure out flywheel torque. Well, yes and no.
It turns out that all the dyno needs to know is engine RPM. It does not matter whether the dyno is run up quickly with a relatively large drive-wheel torque (DWT) or run up slowly with a relatively small DWT. Furthermore, the radius of the driving wheels and tyres also does not matter. Here's why.
Wheel RPM is directly proportional to drum RPM, assuming the longitudinal
slip of the tyres is within a small range. The reason is that at the point of
contact, the drum and wheel have the same circumferential (longitudinal,
tangential) speed, so ![]() . Let's write
. Let's write ![]() , where
, where ![]() . Engine RPM
is related to wheel RPM by a factor that depends on the final-drive gear ratio f
and the selected gear ratio
. Engine RPM
is related to wheel RPM by a factor that depends on the final-drive gear ratio f
and the selected gear ratio ![]() . We write
. We write ![]() . Usually,
engine RPM is much larger than wheel RPM, so we can expect
. Usually,
engine RPM is much larger than wheel RPM, so we can expect ![]() to be larger
than 1 most of the time. So, we get
to be larger
than 1 most of the time. So, we get
![]()
We also know that, by Newton's Third Law, that the force applied to the drum by the tyre is the same as the force applied to the tyre by the drum. Therefore the torques applied are in proportion to the radii of the wheel + tyre and the drum, namely that
![]()
or ![]() . Recalling that the transmission gear and final drive multiply
engine torque, we also know that
. Recalling that the transmission gear and final drive multiply
engine torque, we also know that ![]() , so
, so ![]() . But we
already know
. But we
already know ![]() : it's the ratio of the RPMs, so
: it's the ratio of the RPMs, so ![]() , or, more
usefully,
, or, more
usefully,
![]()
Every term on the right-hand side of this equation is measured or known by
the dyno, so we can measure engine torque independently of car details! We can
even plot ![]() versus
versus ![]() , effectively taking the run-up time and the drum data
out of the report.
, effectively taking the run-up time and the drum data
out of the report.
Almost. There is a small gotcha. The engine applies torque indirectly to the drum, spinning it up. But the engine is also spinning up the clutch, transmission, drive shaft, differential, axles, and wheels, which, all together, have an unknown moment of inertia that varies from car-to-car, though it's usually considerably smaller than J, the moment of inertia of the drum. But, in the equations of motion, above, we have not accounted for them. More properly, we should write
![]()
This doesn't help us much because we don't know ![]() , so we pull a
fast one and rearrange the equation:
, so we pull a
fast one and rearrange the equation:
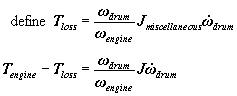
This is why chassis dyno numbers are always lower than test-stand dyno
numbers for the same engine. The chassis dyno measures ![]() , and the
test-stand measures
, and the
test-stand measures ![]() . Of course, those trying to sell engines often report
the best-sounding numbers: the test-stand numbers. So, don't be disappointed
when you take your hot, new engine to the chassis dyno after installation and
get numbers 15% to 20% lower than the advertised 'at the crankshaft' numbers in
the brochure. It's to be expected. Typically, however, you simply do not
know
. Of course, those trying to sell engines often report
the best-sounding numbers: the test-stand numbers. So, don't be disappointed
when you take your hot, new engine to the chassis dyno after installation and
get numbers 15% to 20% lower than the advertised 'at the crankshaft' numbers in
the brochure. It's to be expected. Typically, however, you simply do not
know ![]() : it's a number you take on faith.
: it's a number you take on faith.
Let's run a quick sample. The following numbers are pulled out of thin air,
so don't hang me on them. Suppose the drum has 3-foot radius, is solid, and
weighs 6,400 lbs, which is about 200 slugs (remember slugs? One slug of mass
weighs about 32 pounds at the Earth's surface). So, the moment of inertia of the
drum is about ![]() . Let's say that the engine takes about 15 seconds to
run from 1,500 RPM to 6,000 RPM in fourth gear, with a time profile like the
following:
. Let's say that the engine takes about 15 seconds to
run from 1,500 RPM to 6,000 RPM in fourth gear, with a time profile like the
following:
| t | e RPM | V MPH | v FPS | drum |
drum |
drum RPM | RPM ratio | Torque |
| 0 | 1,500 | 35 | 51.33 | 17.11 | 0.00 | 163.40 | 0.1089 | 0.00 |
| 1 | 1,800 | 42 | 61.60 | 20.53 | 3.42 | 196.08 | 0.1089 | 335.51 |
| 2 | 2,100 | 49 | 71.87 | 23.96 | 3.42 | 228.76 | 0.1089 | 335.51 |
| 3 | 2,400 | 56 | 82.13 | 27.38 | 3.42 | 261.44 | 0.1089 | 335.51 |
| 4 | 2,700 | 63 | 92.40 | 30.80 | 3.42 | 294.12 | 0.1089 | 335.51 |
| 5 | 3,000 | 70 | 102.67 | 34.22 | 3.42 | 326.80 | 0.1089 | 335.51 |
| 6 | 3,300 | 77 | 112.93 | 37.64 | 3.42 | 359.48 | 0.1089 | 335.51 |
| 7 | 3,600 | 84 | 123.20 | 41.07 | 3.42 | 392.16 | 0.1089 | 335.51 |
| 8 | 3,900 | 91 | 133.47 | 44.49 | 3.42 | 424.84 | 0.1089 | 335.51 |
| 9 | 4,200 | 98 | 143.73 | 47.91 | 3.42 | 457.52 | 0.1089 | 335.51 |
| 10 | 4,500 | 105 | 154.00 | 51.33 | 3.42 | 490.20 | 0.1089 | 335.51 |
| 11 | 4,800 | 112 | 164.27 | 54.76 | 3.42 | 522.88 | 0.1089 | 335.51 |
| 12 | 5,100 | 119 | 174.53 | 58.18 | 3.42 | 555.56 | 0.1089 | 335.51 |
| 13 | 5,400 | 126 | 184.80 | 61.60 | 3.42 | 588.24 | 0.1089 | 335.51 |
| 14 | 5,700 | 133 | 195.07 | 65.02 | 3.42 | 620.92 | 0.1089 | 335.51 |
| 15 | 6,000 | 140 | 205.33 | 68.44 | 3.42 | 653.60 | 0.1089 | 335.51 |
The "v MPH" column is just a straight linear ramp from 35 MPH to
140 MPH, which are approximately right in my Corvette. The "v FPS"
column is just 22 / 15 the v MPH. The drum ![]() is in
radians per second and is just v FPS divided by 3 ft, the drum radius. The drum
is in
radians per second and is just v FPS divided by 3 ft, the drum radius. The drum ![]() is just the stepwise difference of the drum
is just the stepwise difference of the drum ![]() numbers. It's constant, as we would expect from a run-up of the dyno at constant
acceleration. The drum RPM is
numbers. It's constant, as we would expect from a run-up of the dyno at constant
acceleration. The drum RPM is ![]() times the drum
times the drum ![]() . The
RPM ratio is just drum RPM divided by engine RPM, and it must be strictly
constant, so this is a nice sanity check on our math. Finally, the torque column
is the RPM ratio times J = 900 slug - ft2
times drum
. The
RPM ratio is just drum RPM divided by engine RPM, and it must be strictly
constant, so this is a nice sanity check on our math. Finally, the torque column
is the RPM ratio times J = 900 slug - ft2
times drum ![]() . We see a constant torque output of about 335
ft-lbs. Not bad. It implies a test-stand number of between 394 and 418,
corresponding to 15% and 20% driveline loss, respectively. Looks like we nailed
it without 'cooking the books' too badly. Of course, we have a totally flat
torque curve in this little sample, but that's only because we have a completely
smooth ramp-up of velocity.
. We see a constant torque output of about 335
ft-lbs. Not bad. It implies a test-stand number of between 394 and 418,
corresponding to 15% and 20% driveline loss, respectively. Looks like we nailed
it without 'cooking the books' too badly. Of course, we have a totally flat
torque curve in this little sample, but that's only because we have a completely
smooth ramp-up of velocity.
Dyno reports often will be labelled 'Rear-wheel torque' (RWT) or, less prejudicially, 'drive-wheel torque' (DWT) to remind the user that there is an unknown component to the measurement. These are well intentioned misnomers: do not be mislead! What they mean is 'engine torque as if the engine were connected to the drive wheels by a massless driveline', or 'engine torque as measured at the drive wheels with an unknown but relatively small inertial loss component'. It should be clear from the above that the actual drive-wheel torque cannot be measured without knowing A, the ratio of the drum radius to the wheel + tyre radius. It's slightly ironic that an attempt to clear up the confusion risks introducing more confusion.
In the next instalment, we relate the equations of motion for the driving wheel to the longitudinal magic formula to compute reaction forces and get equations of motion for the whole car.
References:
http://www.c5-corvette.com/DynoJet_Theroy.htm
[sic]
http://www.mustangdyne.com/pdfs/7K
manualv238.pdf
http://www.revsearch.com/dynamometer/torque_vs_horsepower.html
Attachments:
I've included the little spreadsheet I used to simulate the dyno run. It can be downloaded here.
ERRATA:
* Part 14, yet again, the numbers for frequency are actually in radians per
second, not in cycles per second. There are ![]() cycles per
radian, so the 4 Hz natural suspension frequency I calculated and then tried to
rationalize was really 4 / 6.28 Hz, which is quite reasonable and not requiring
any rationalization. Oh, what tangled webs we weave…
cycles per
radian, so the 4 Hz natural suspension frequency I calculated and then tried to
rationalize was really 4 / 6.28 Hz, which is quite reasonable and not requiring
any rationalization. Oh, what tangled webs we weave…
* Physical interpretations of slip on page 2 of part 24: "Car (hub) moving forward, CP moving slowly forward w.r.t. ground, resisting car motion." Should be "Car (hub) moving forward, CP moving slowly forward w.r.t. HUB, resisting car motion."
* Part 21, in the back-of-the-envelope numerical calculation just before the 3-D plot at the end of the paper, I correctly calculated tan-1(0.8222) = 0.688, but then incorrectly calculated tan-1(SB) - SB as -0.266. Of course, it's 0.688 - 0.822 = -0.134. One of the hazards of doing math in one's head all the time is the occasional slip up. Normally, I check results with a calculator just to be really sure, but some are so trivial it just seems unnecessary. Naturally, those are the ones that bite me.